平行四辺形から これら、対角線をはさむ二つの平行四辺形を 除いて残る 二つの平行四辺形をいう。 (以下、定義の補足(命題1-43)(対角線をはさむ平行四辺形・補形)という。) 命題1-44作図線分,三角形,直線角と平行四辺形)こんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定義とは まず、「平行四辺形とは何か」口で説明平行四辺形 (へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ 平行 である 四角形 のことである。

標準 平行線と平行四辺形の個数 なかけんの数学ノート
平行四辺形とは
平行四辺形とは-平行四辺形の対角線CE)の過小視の組 F E'・ D' ・ み合わせにより生じた。 。 さて,本論の実験は, Metzgerの説を Fig 1ザンダーの平行四辺形(ザンダー錯視) さらに精神物理学的に検討するためにA 22 + 2 ×



1
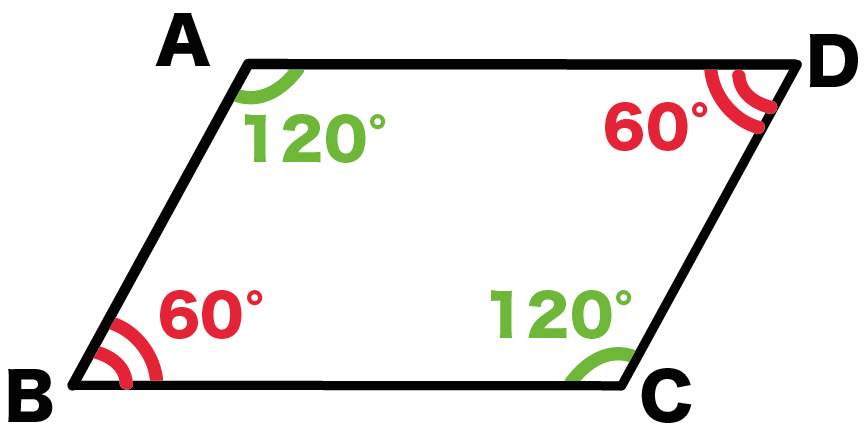
平行四辺形は2つの 合同 な 三角形 を2つ、対応するひと組の辺を共有し、その両端の頂点が対応と逆順に重なるように並べた図形である。 三角形の面積を 〔底辺〕×〔高さ〕÷2 で表すことができるのは、それが平行四辺形の面積を2等分して求めた結果だ平行四辺形 ( parallelogram ) 2組の対辺がそれぞれ 平行 である四角形。 対辺は(2組あるが、それぞれ)長さが等しくなっている。 対角は(2組あるが、それぞれ)大きさが等しくなっている。 対角線は(2本あるが、そのどちらも)他の対角線の中点を通る。結論を述べると,2次正方行列の行列式は平行四辺形の面積である. 下図を見て欲しい.行列 A の1列目が橙色ベクトル,2列目が緑色ベクトルで,それらを2辺とする平行四辺形の面積が行列式 A だ.これは簡単に示すことができる.平行四辺形を含む長方形の面積から,平行四辺形の外側
特別な平行四辺形 つまり,平行四辺形に 「4つの角が等しい (1つの角が90°)」 という特徴を加えると, 長方形 になります。 「4つの辺が等しい」 という特徴を加えると, ひし形 になります。1組の対辺が平行な四角形は 台形 なので,平行 四辺形 は台形の特別な場合とみなすことができる。 また,2本の対角線の 交点 を中心として 点対称 な 図形 であり,この中心は平行四辺形の 重心 と一致すA 21) ) = a 11 ×
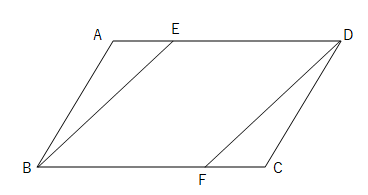
平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。平行四辺形 ひし形 台形 年 組 名前 3定 じょう ぎや分度器ではからずに、平行四辺形の辺の長さや角度を求 もと めましょう。 2平行四辺形をかきましょう。 ①平行な直線を使って、平行四辺形を かきましょう。 例 れい ② 方がん(ます)を使って、平行四平行四辺形である。 , 定義の補足(命題1ー34)(平行四辺形・対角線) による。 EBCA、DBCF;平行四辺形 となっている。 しかも等しい。 ・・・(2) なぜなら 同じ底辺BCの上にあり かつ
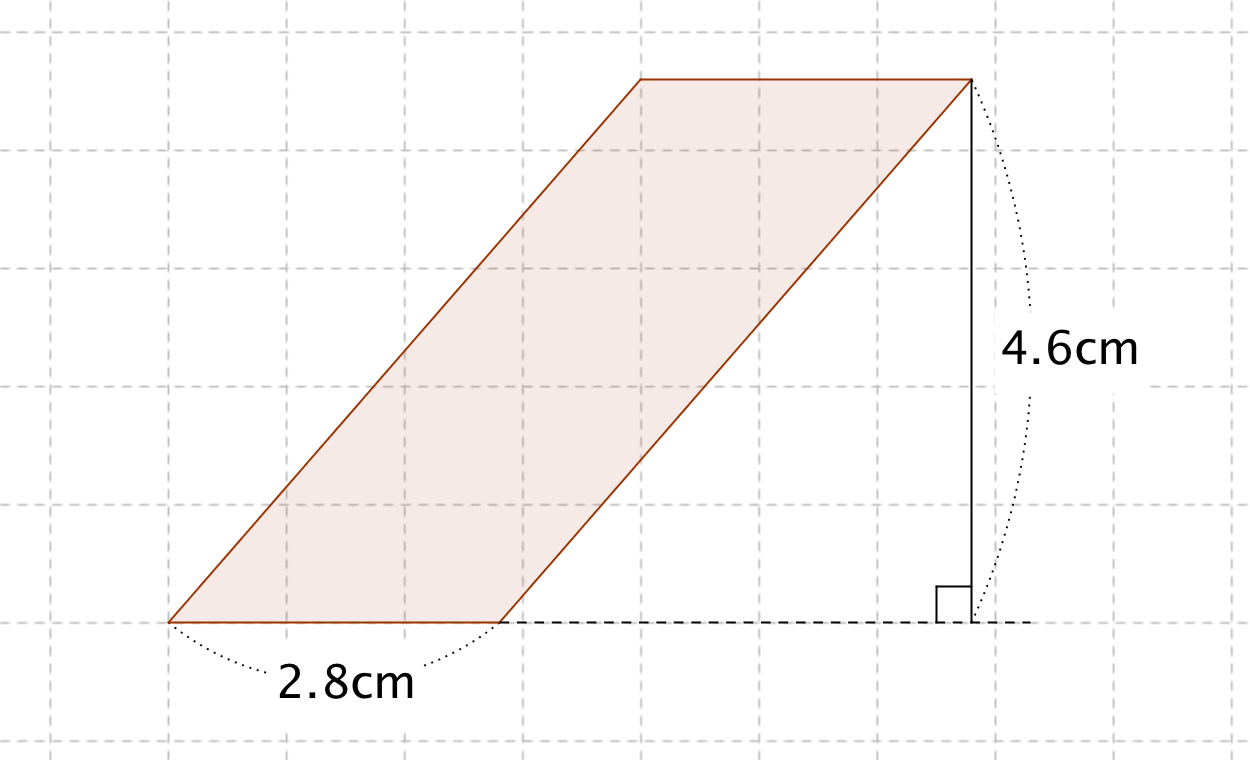



平行四辺形の面積の公式 算数の公式




簡単公式 平行四辺形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
三角関数をやっていて高校数学に興味が出てきた。 それをジオジェブラでやったらもっとわかりやすくなるのではないかと。 そこで、ベクトルについてやってみることにした。 ベクトルと複素数と三角関数は密接な関係があることがわかってきた。 そこで静力学と結びつけることにしたが4点0,2ω 1 ,2ω 2 ,2ω 1 +2ω 2 を頂点とする平行四辺形を基本周期平行四辺形という。 歴史的には,楕円関数の研究は,楕円積分に源をもつ。 ※「基本周期平行四辺形」について言及している用語解説の一部を掲載しています。平行四辺形の面積は dbcを2倍した値になるので24となります。 以上より rpqの面積を1としたとき、平行四辺形abcdの面積は24となるので 答えは24倍 となります。 ちょっと難しかったけど これも面積比を確実に見ていけば大丈夫な問題ですね! まとめ



1
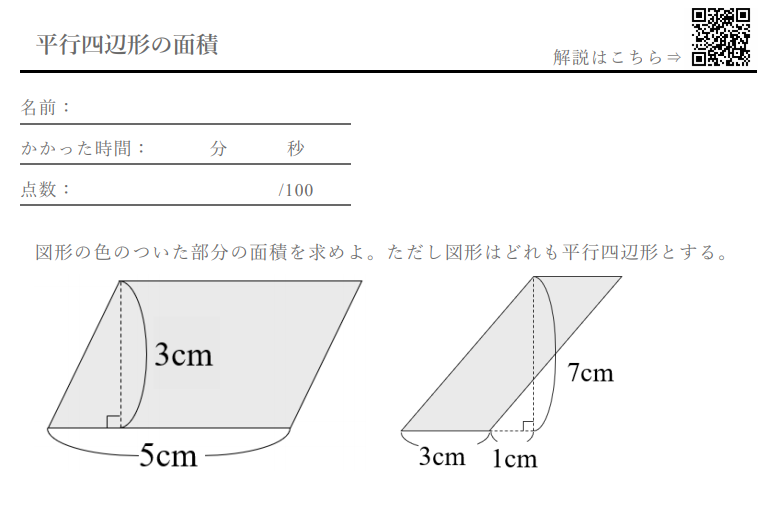



平行四辺形 の面積 計算ドリル 問題集 数学fun
平行四辺形とひし形の違いってなに??←今回の記事 平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介!平行四辺形の頂点の座標 平行四辺形の性質を利用して、頂点の座標を求める方法を学びましょう。 点A(-1,3)、点B(3,3)、点C(5,-1)、点D(x,y)の4つの点を頂点とする平行四辺形ADCBがあるとき、点Dの座標を求めなさい 平行四辺形解答 平行四辺形abcd を¢abcdと 書くことがある。 ab¿dc 平行四辺形




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
(a 12 + a 22 ) ー( a 11 ×台形,平行四辺形,ひし形 (1)台形と平行四辺形 右の平行四辺形で,辺アイ,アエはそれぞれ何cmでしょう。 また,角ア,ウ,エの角度はそれぞれ何度でしょう。 角ウ (2)ひし形 向かい合った1組の辺が平行な四角形を といいます。まずは、平行四辺形と呼ばれる図形とはどのようなものなのかを説明していきます。 平行四辺形とは、「 2組の向かい合う辺 (対辺)が、それぞれ平行な四角形 」のことを指します。
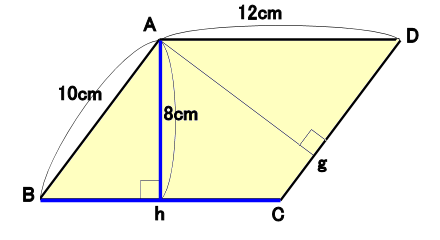



平行四辺形と高さ




平行四辺形 Wikipedia
行列式 線型代数 数学教育 二つのベクトル v 1, v 1 が張る平行四辺形の面積を考える: v 1, v 1 を数ベクトルに表す: 平行四辺形の面積は,つぎの計算で求められる: (a 11 + a 21 ) ×平行四辺形 (へいこうしへんけい、英 parallelogram)とは、2組の対辺がそれぞれ 平行 である 四角形 のことである。平行四辺形の面積の公式 平行四辺形の底辺を 、高さを 、斜辺を 、底辺と斜辺のなす角を とおくと、面積 は




平行四辺形の辺や角を求める Youtube



平行四辺形とは 1分でわかる意味 定義 角度 面積 長方形と正方形との関係
A 12 + a 21 ×平行四辺形( へいこうしへんけい 、 英 parallelogram )とは、 2組 の 対辺 が それぞれ 平行 である 四角形の ことで ある。2組の対辺が平行ならば、対角線がそれぞれ の中点で交わることの証明 仮定 結論 b c a d ab//cd tab//bc ao=co tbo=do aboと cdoにおいて 平行四辺形の対辺は等しいから ab=cd ・・・① 平行線の錯角は等しいので ab//cdより ∠abo=∠cdo・・・② ∠bao=∠dco・・・③




2次の正方行列式と平行四辺形の面積 機械学習に詳しくなりたいブログ




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室
平行四辺形は2つの 合同 な 三角形 を2つ、対応するひと組の辺を共有し、その両端の頂点が対応と逆順に重なるように並べた図形である。 三角形の面積を 〔底辺〕×〔高さ〕÷2 で表すことができるのは、それが平行四辺形の面積を2等分して求めた結果だ1平行四辺形とは? 平行四辺形は、向かい合う2組の辺が平行な四角形です。 ある四角形について,①2組の対辺がそれぞれ平行であると示せば,平行四辺形であることが証明できるのはわかりますね。 2ポイント ただし,「2組の対辺が平行=平行四辺形」と覚えるだけでは,平行四辺形のスポンサーリンク 平行四辺形の面積 \(=\) 底辺 \(\times\) 高さ それでは「平行四辺形の面積の公式」を使った「練習問題」を解いてみましょう。「公式の考察」についても合わせてみていきます。 練習問
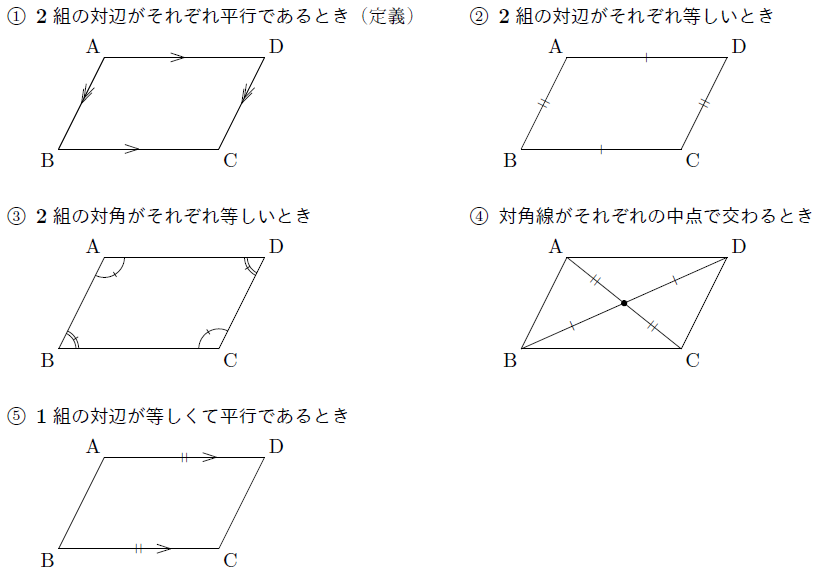



平行四辺形になるための条件 まなびの学園
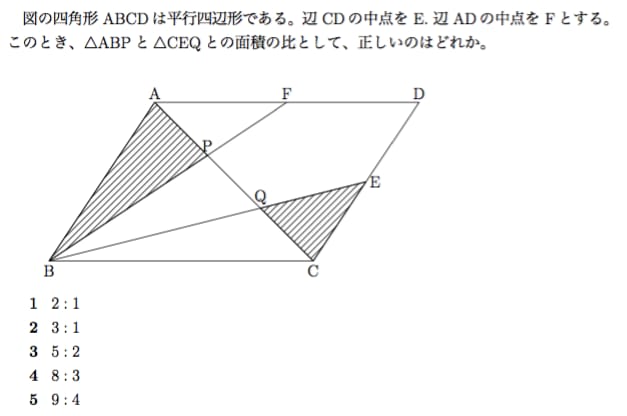



平行四辺形 中点 2つの三角形の面積比 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください
平行四辺形の対辺だから,ab=cd ab¿dc より,~bae=~dcf 2組の辺とその間の角がそれぞれ等しいから,∑abe«∑cdf 例題 a e f d b c ¢平 行 四 辺 形(へいこうしへんけい) 二組の対辺が共に 平行である四角形。 発音 へ↗ーこーしへ↘んけー 関連語 四角形, 四辺形, 方形, 角形, 枡形, 升形, 斗形;
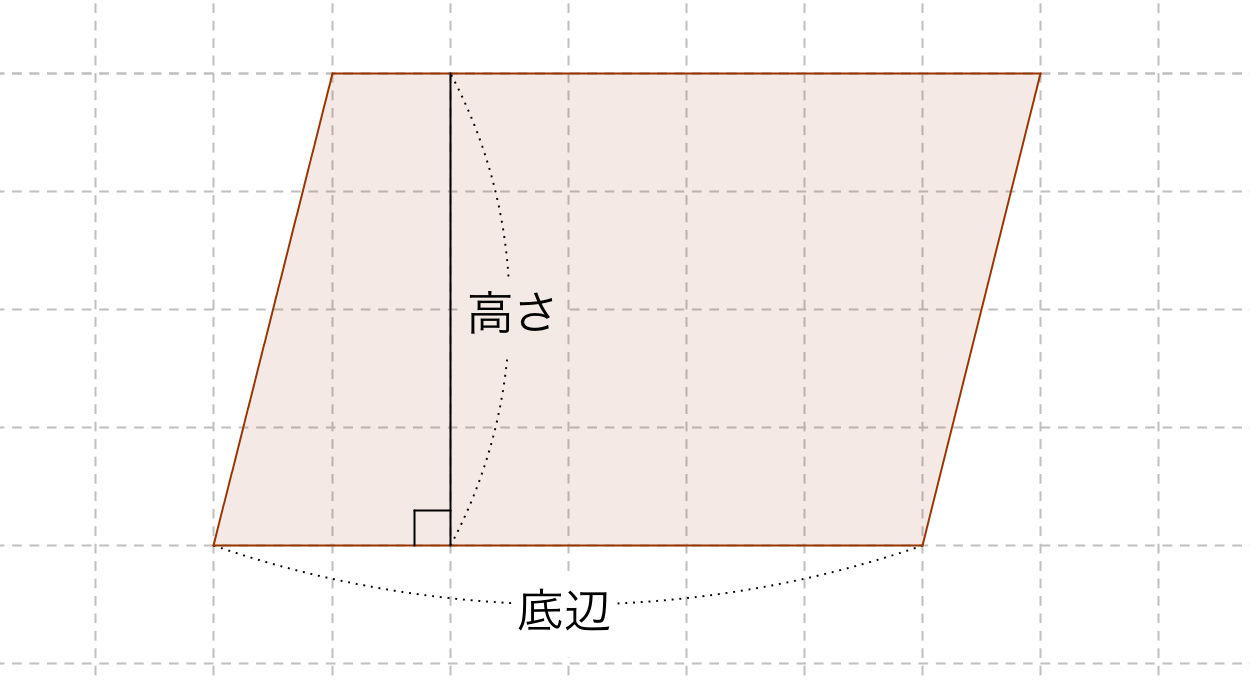



平行四辺形の面積の公式 算数の公式
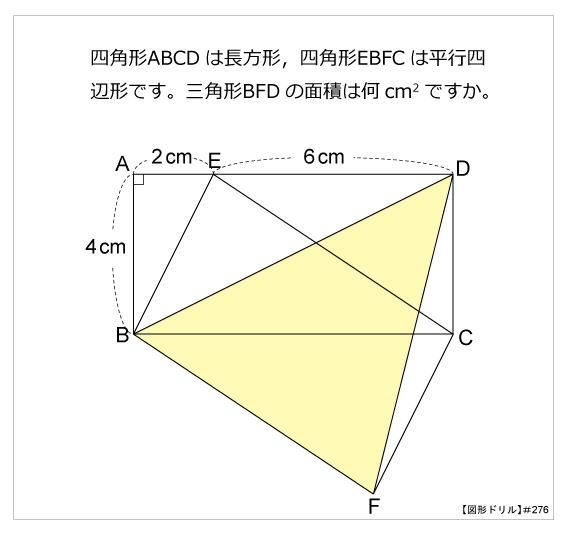



図形ドリル 第276問 長方形と平行四辺形 算数星人のweb問題集 中学受験算数の問題に挑戦




平行四辺形になることの証明 Youtube




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
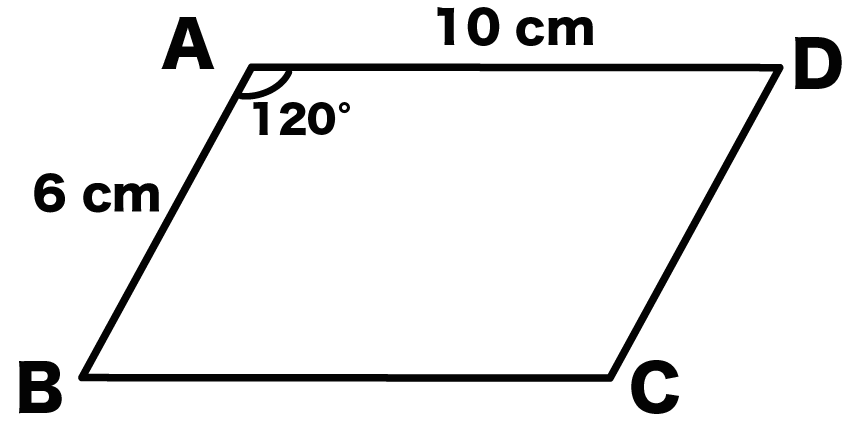



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



中2数学 平行四辺形の証明のポイントと練習問題 Examee



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく



数学b 平行四辺形とベクトルの求め方とコツ ページ 2 教科書より詳しい高校数学




中2数学 平行四辺形であるための条件 例題編 映像授業のtry It トライイット



平行四辺形と頂点
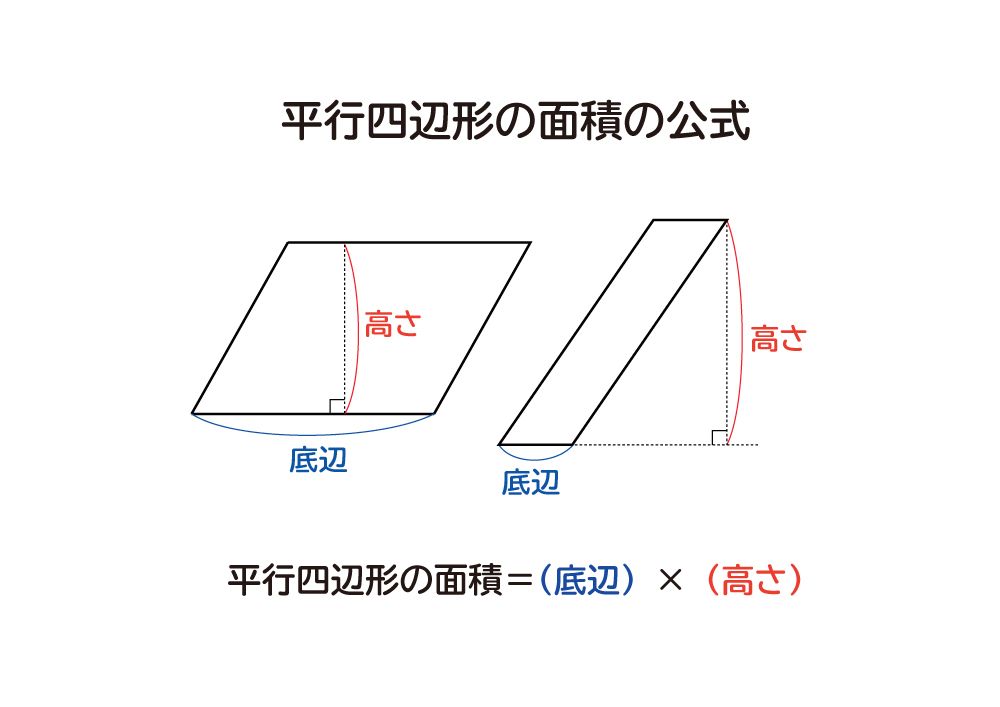



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル
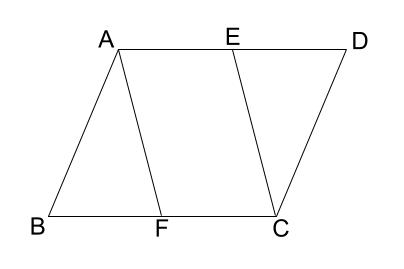



中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su




平行四辺形abcdでbp Pc 2 1 Bpqの面積が4cm のとき Abq Clear
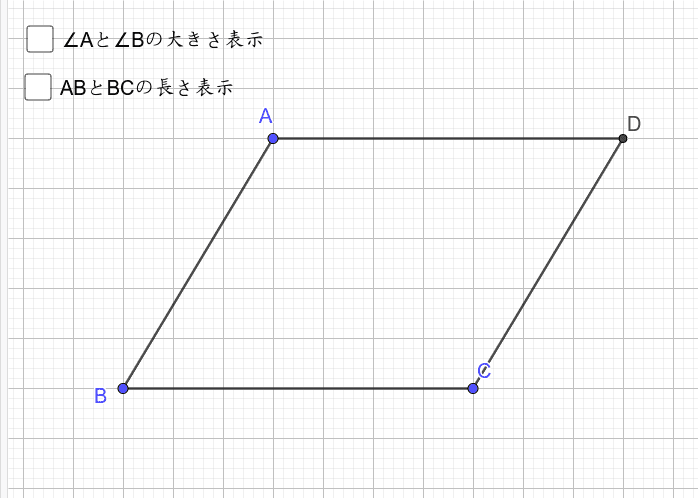



中2 平行四辺形 特別な平行四辺形 Geogebra




ファイル 平行四辺形の説明 Png Wikibooks




平行四辺形の対角線の長さの求め方
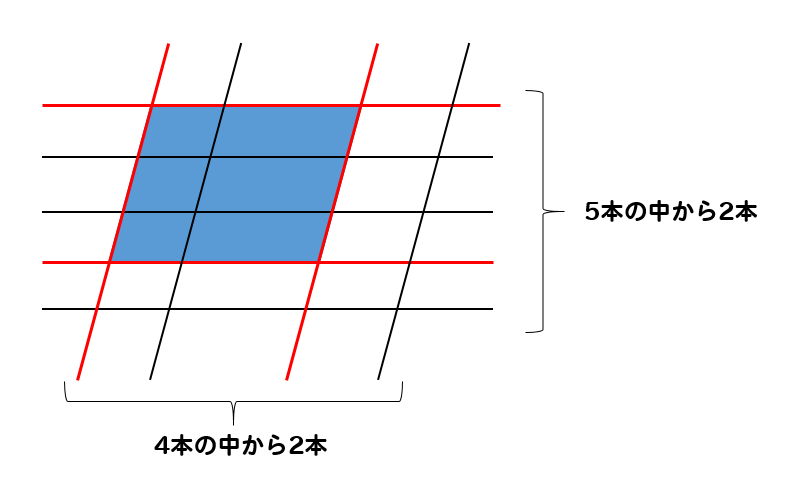



場合の数 平行四辺形は何個ある いくつある 考え方を解説 数スタ
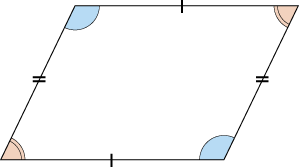



平行四辺形の性質 5年生 算数の広場




関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット




ファイル 平行四辺形の面積1 Png Wikibooks
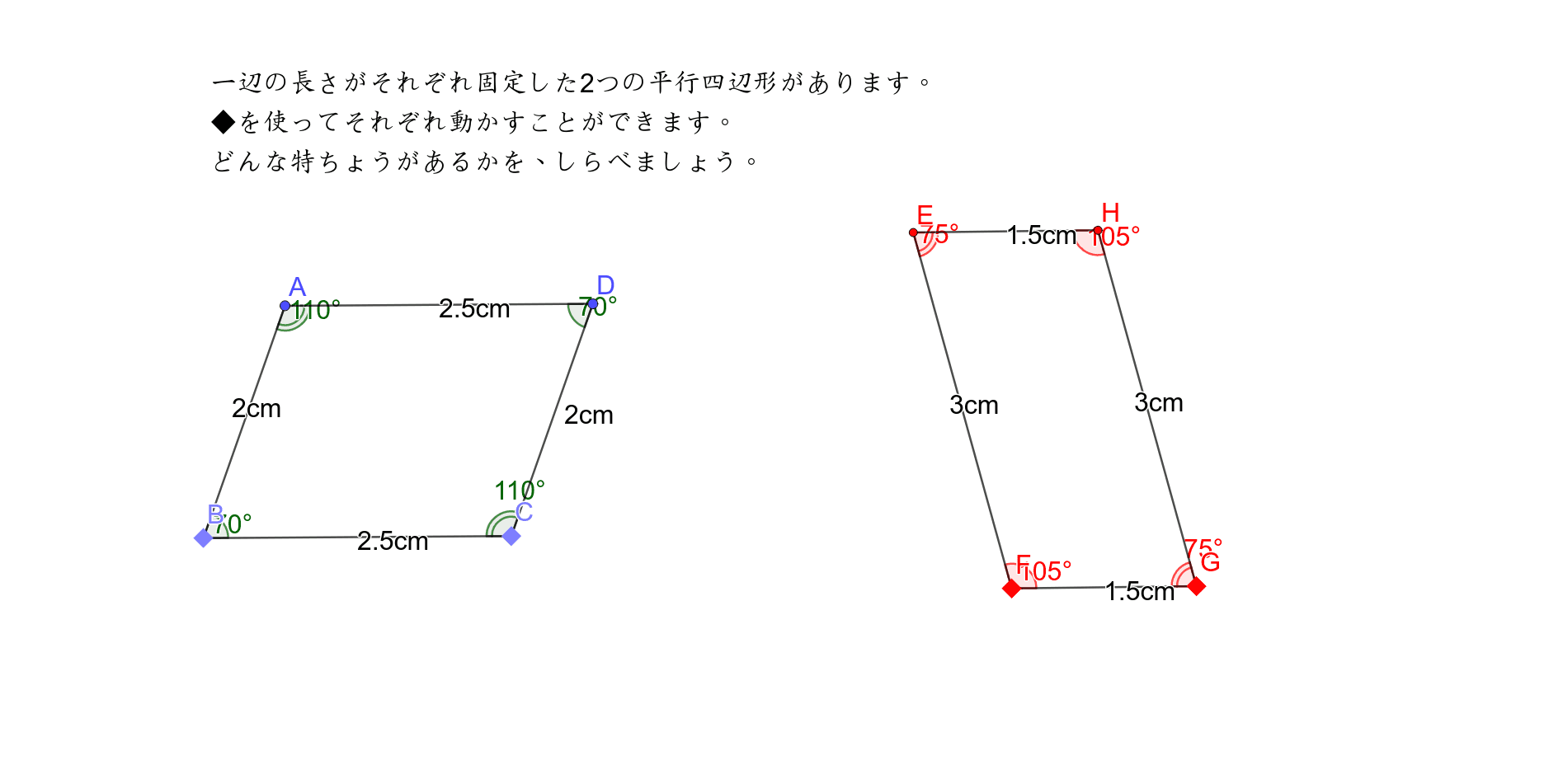



小学4年 平行四辺形にはどんな特徴がありますか Geogebra




平行四辺形の面積を求める公式 あまり知られていないかも 中学や高校の数学の計算問題
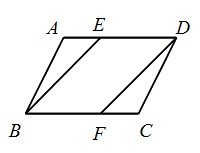



Math 平行四辺形 平行四辺形になることの証明 働きアリ




Math 平行四辺形 平行四辺形になることの証明 働きアリ




平行四辺形と証明 Youtube




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
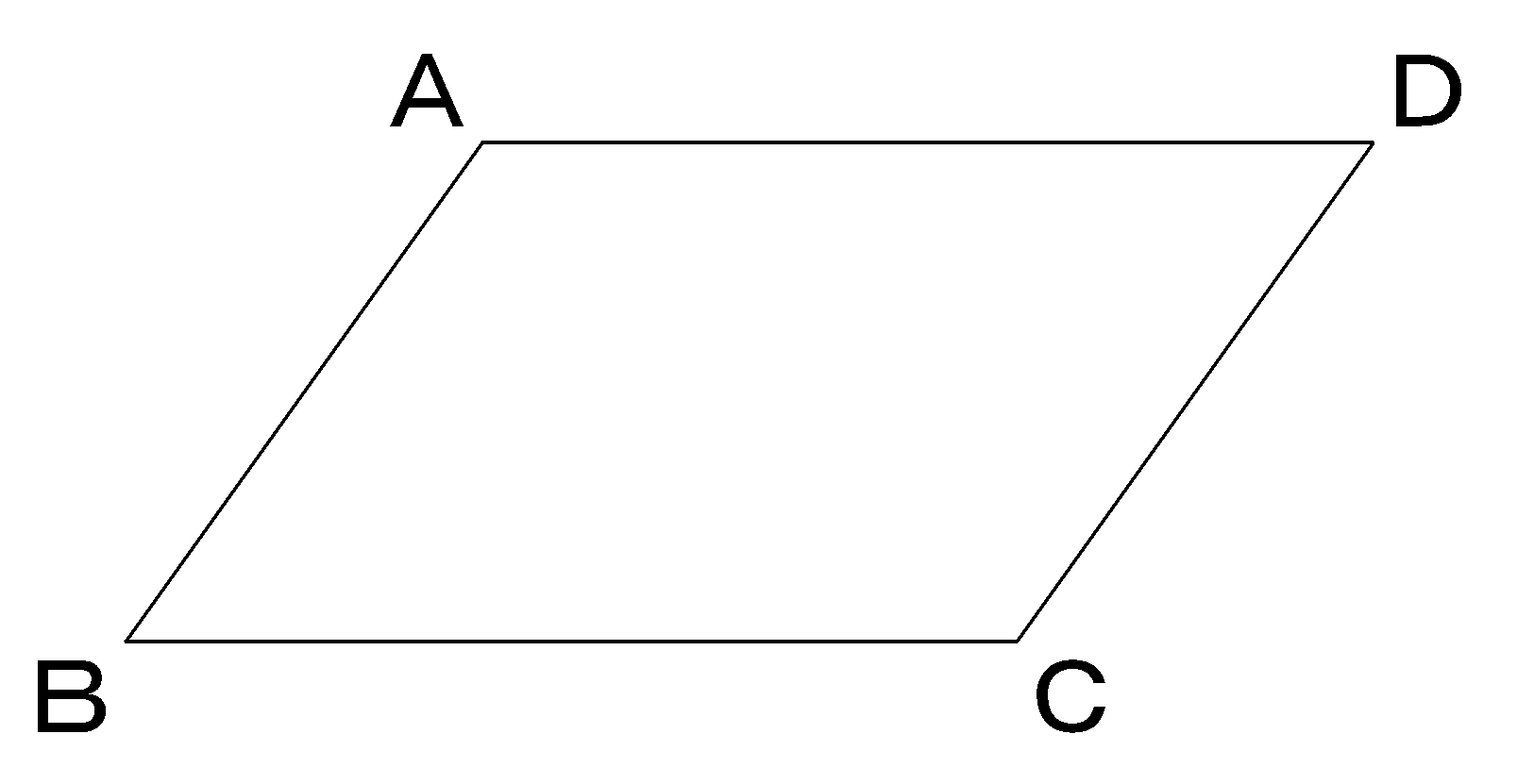



Wordで使える平行四辺形 1 Wordで数学問題プリントを作ろう
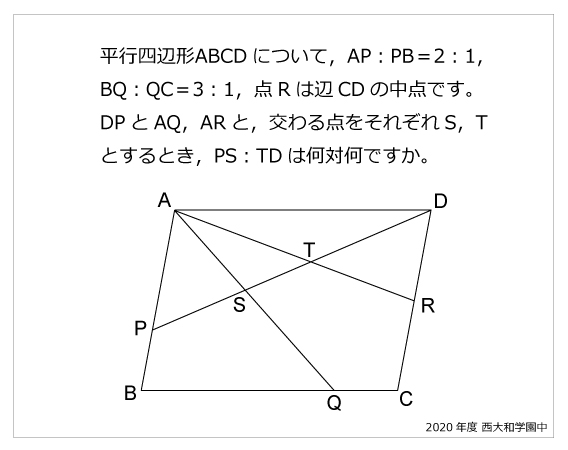



今年の1問 年西大和学園中 平行四辺形と比 算数星人のweb問題集 中学受験算数の問題に挑戦




平行四辺形の面積の求め方 公式と計算例



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形 Wikipedia



4年算数 垂直 平行と四角形 2 教え方
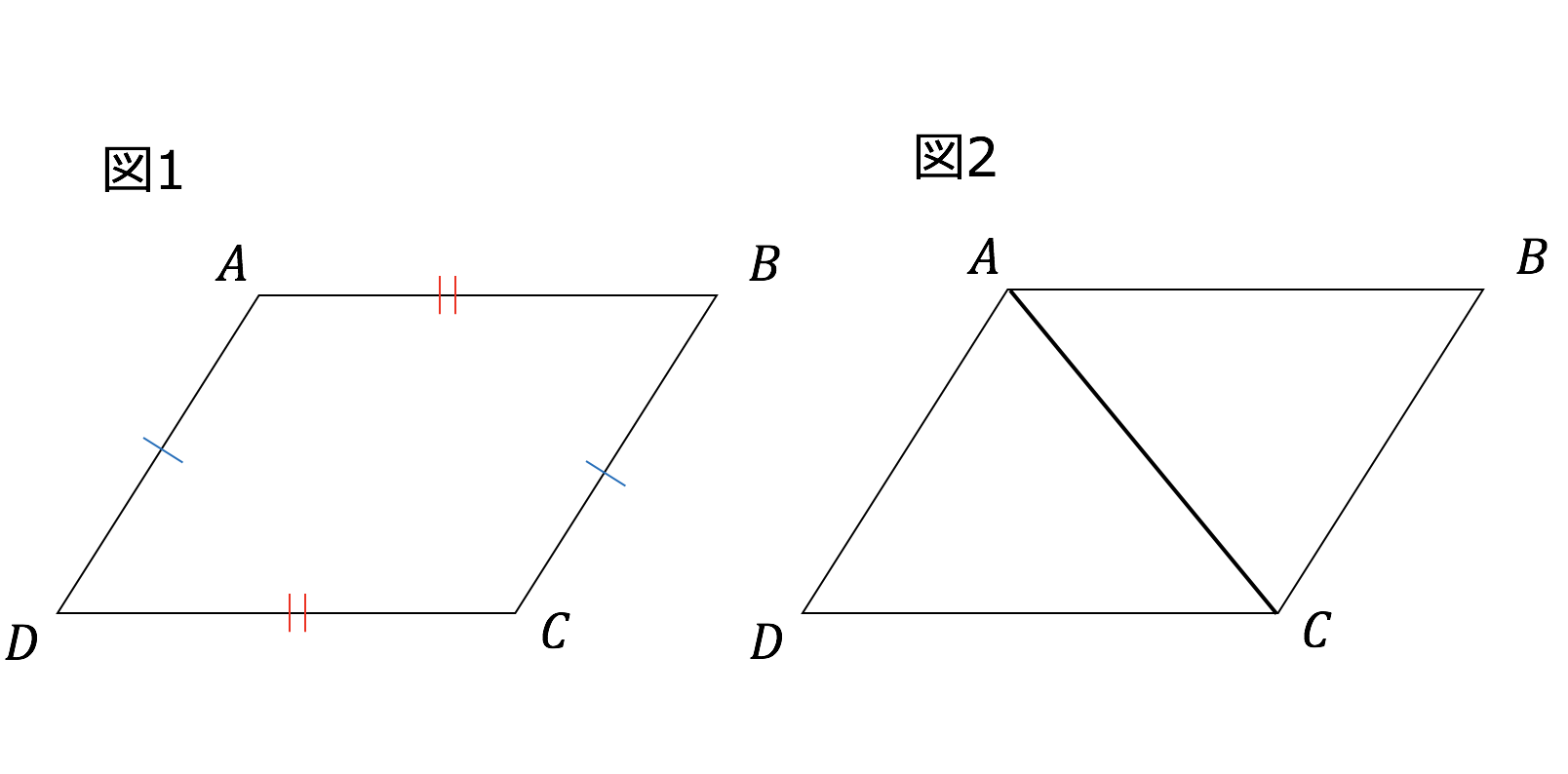



3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ
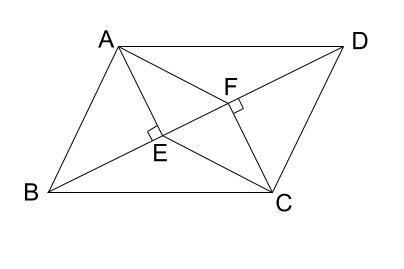



中学数学 平行四辺形になることの証明 その2 中学数学の無料オンライン学習サイトchu Su




平行四辺形の面積の求め方 公式と計算例
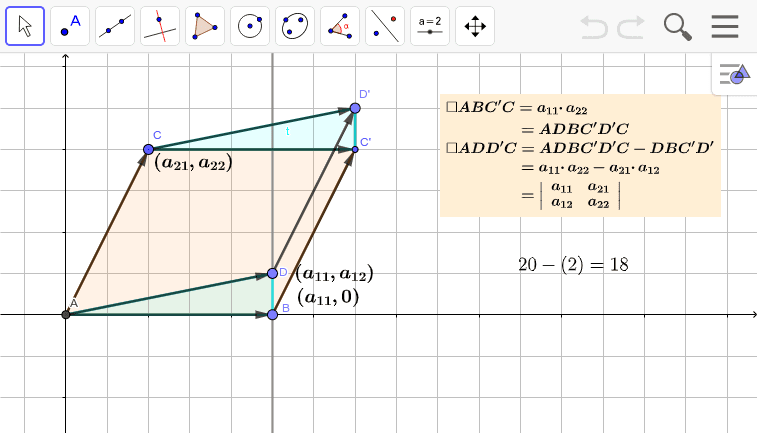



平行四辺形の面積と行列式 Geogebra



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生




3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく
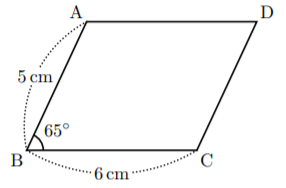



Emath講座 平行四辺形の作図 数樂管理人のブログ



平面図形の基礎



平行四辺形の対角線の折曲げは ねこの耳 から考えよう 算数数学が苦手な子専門のプロ家庭教師みかん先生
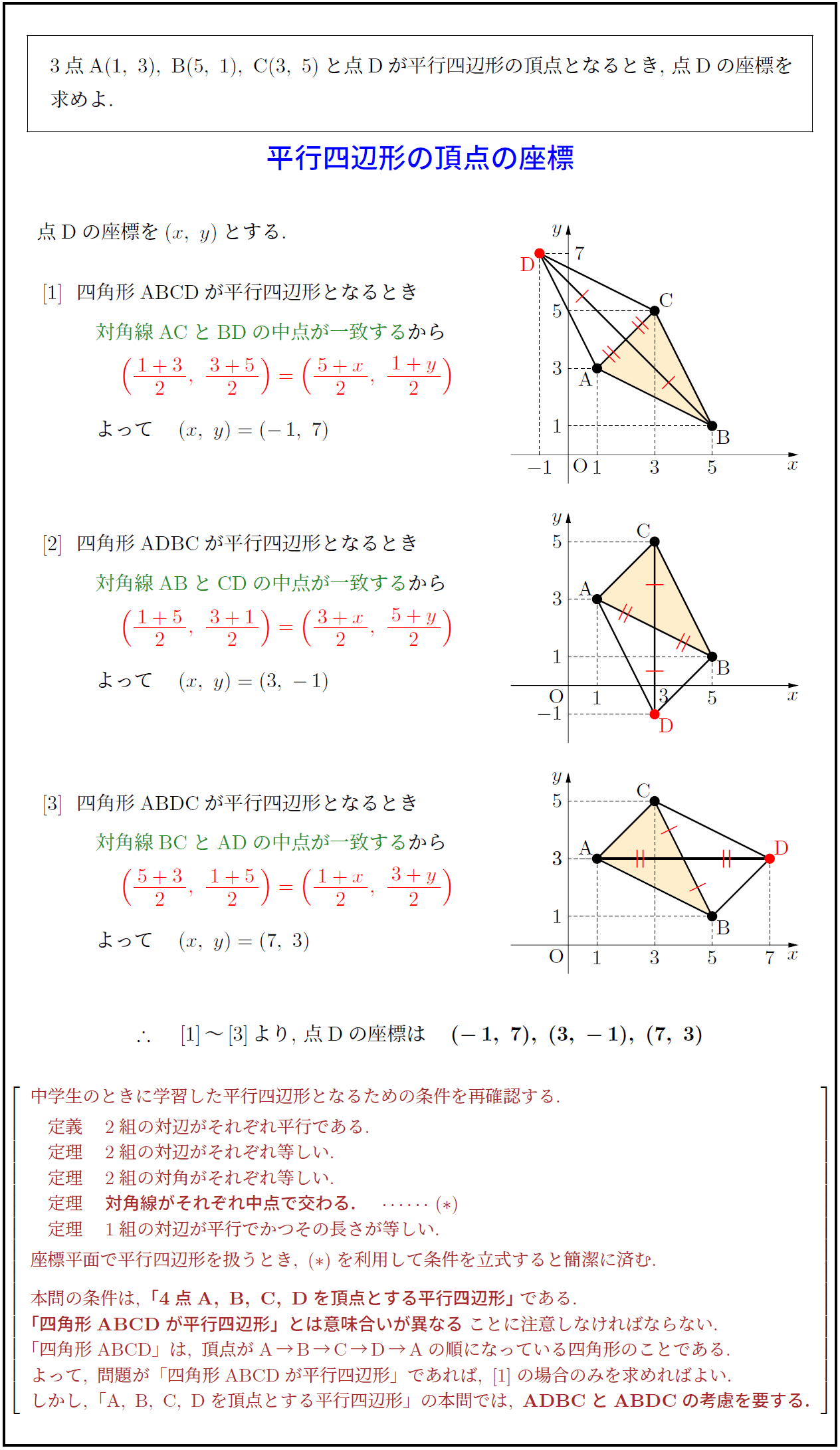



高校数学 平行四辺形の頂点の座標 受験の月




平行四辺形 中学数学で遊ぶ 身勝手な主張



3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく




平行四辺形になるための条件 Youtube




平行四辺形の辺や角を求める Youtube




中2 数学 平行四辺形になるための条件 なんでこうなるのかが わかりません Clear



1




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題
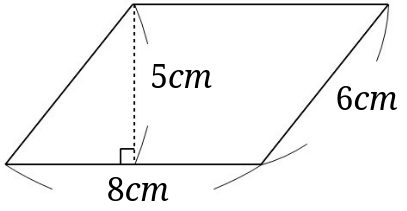



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校



1



平行四辺形とは 1分でわかる意味 定義 角度 面積 長方形と正方形との関係
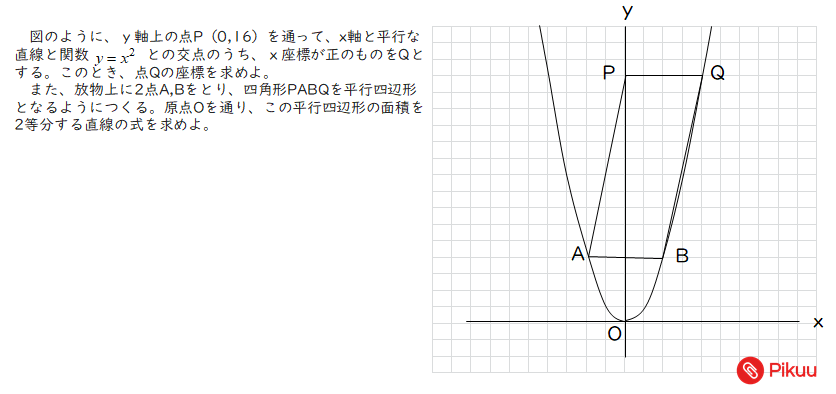



中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



3




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット
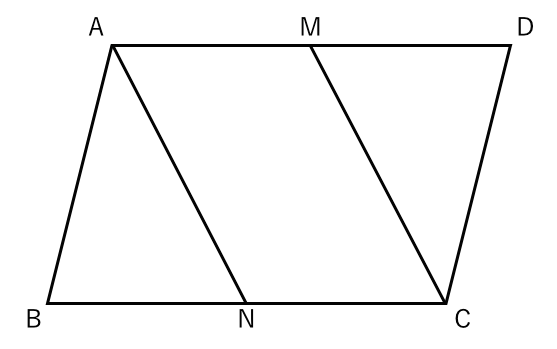



平行四辺形であることを証明する 苦手な数学を簡単に




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
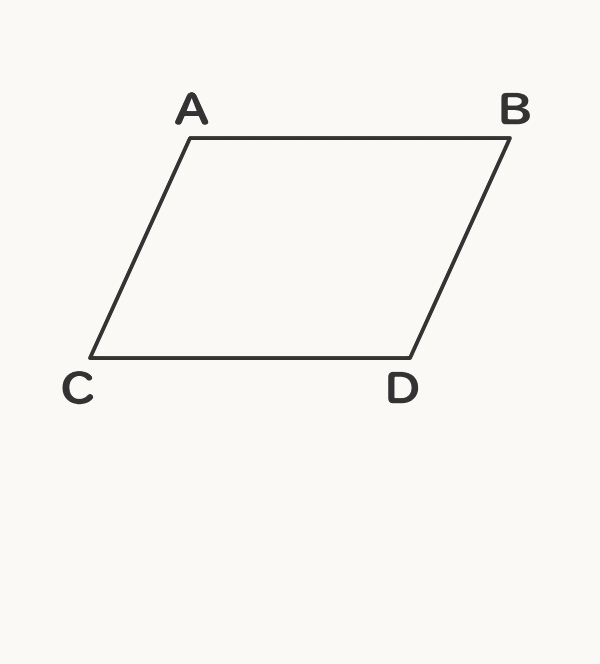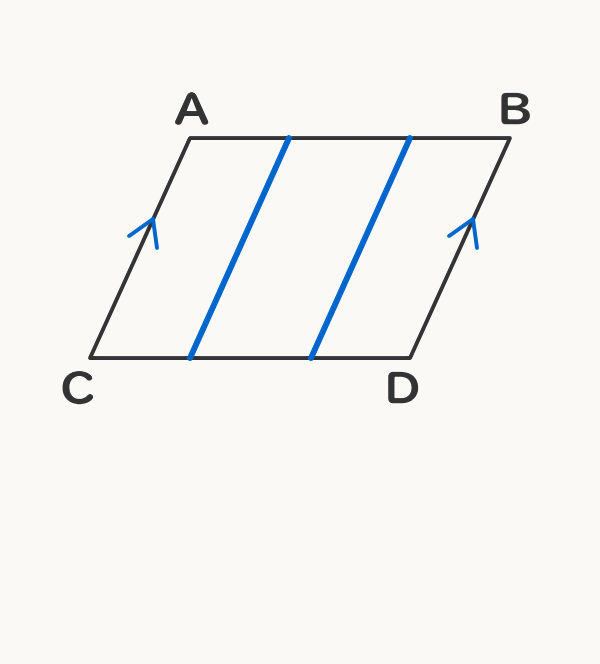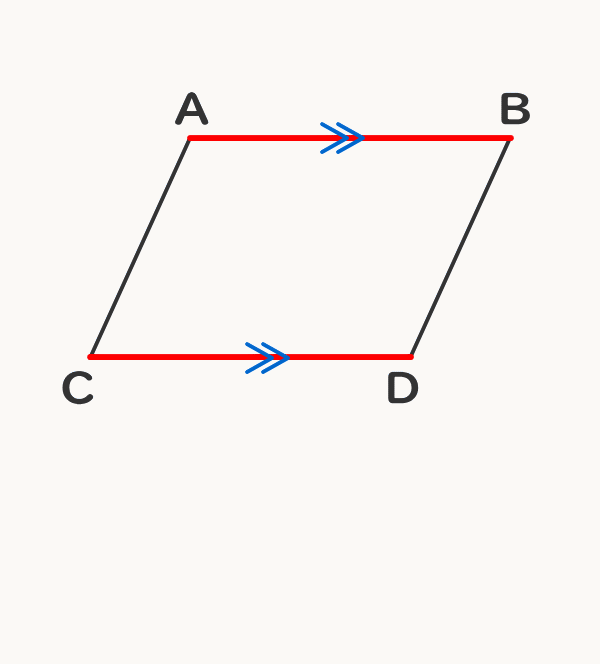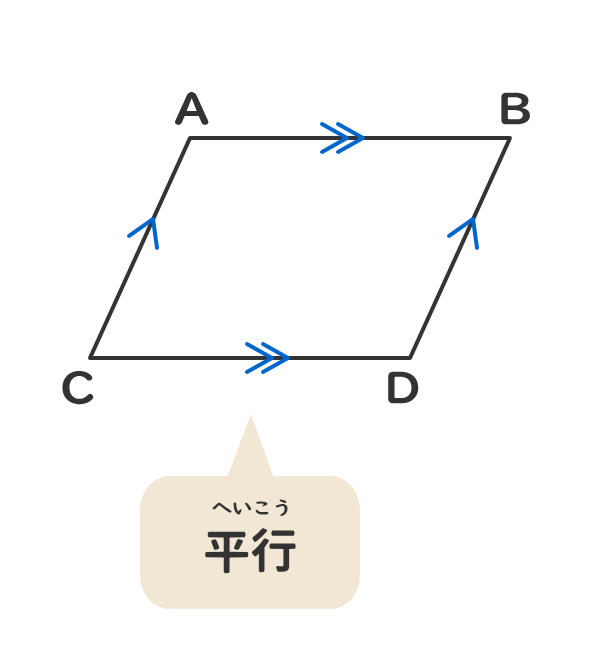



平行四辺形の仲間を知ろう 電験3種web



平行四辺形について知ろう 苦手な数学を簡単に



平行四辺形の性質を使った証明 平行四辺形になることの証明 チーム エン




標準 平行線と平行四辺形の個数 なかけんの数学ノート
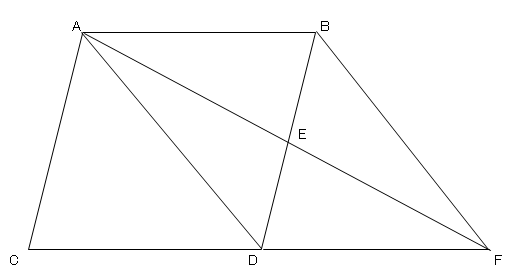



平行四辺形の証明 2 ネット塾




平行四辺形で知っておくべきこと 苦手な数学を簡単に



図形を部分的に加工 調整する 2 平行四辺形など パソコン講師の雑記録



平行 四辺 形 証明 平行四辺形になる条件の証明




平行四辺形の面積の求め方 公式と計算例
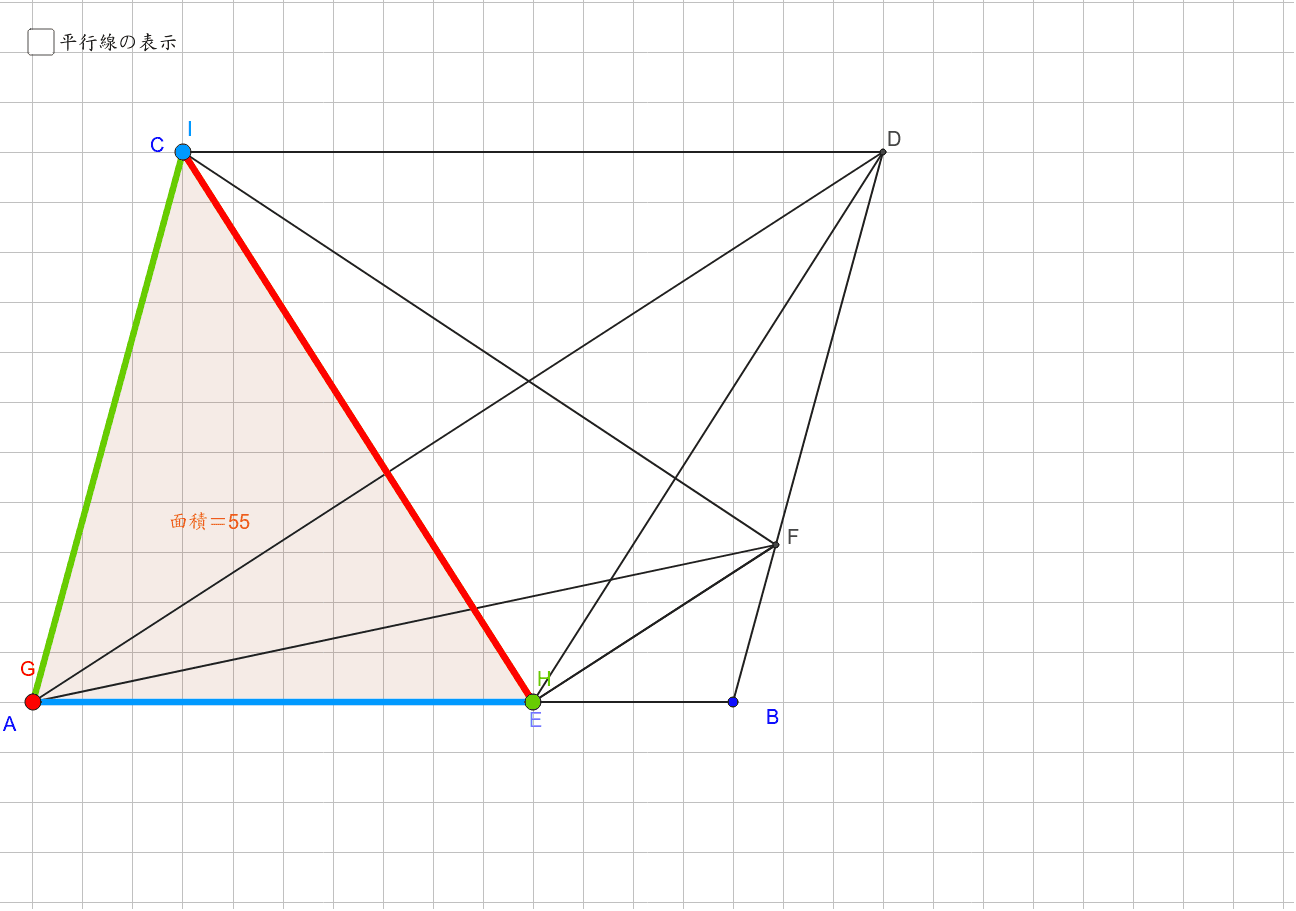



等積変形 平行四辺形 Geogebra




平面図形 平行四辺形は線対称ではないのか 中学数学 定期テスト対策サイト
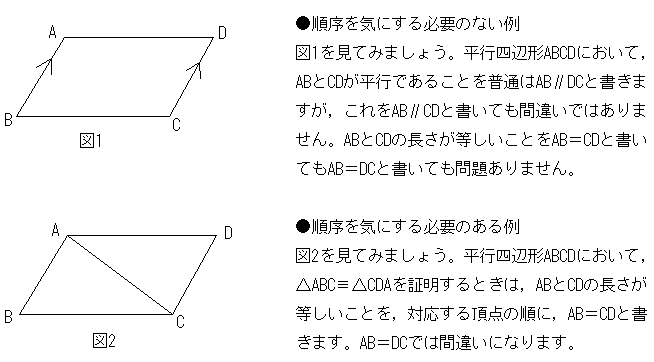



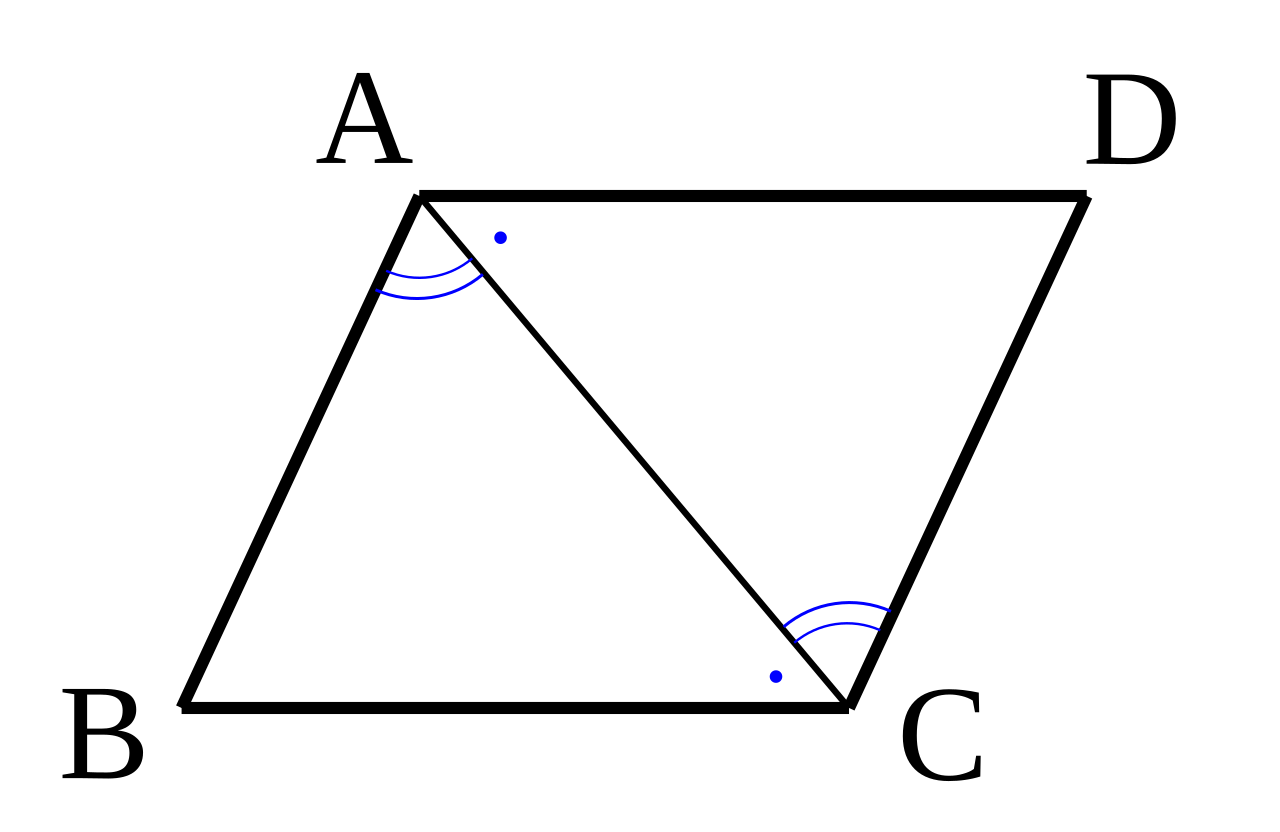
三角形と四角形 平行四辺形の辺や角の表記の順序 中学数学 定期テスト対策サイト




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント



平行四辺形になる条件



平行四辺形の性質1
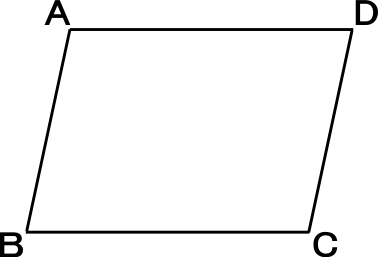



中学2年数学練習問題 図形と合同 平行四辺形の性質と証明問題




平行四辺形の定義と性質 証明問題の解き方 数学fun
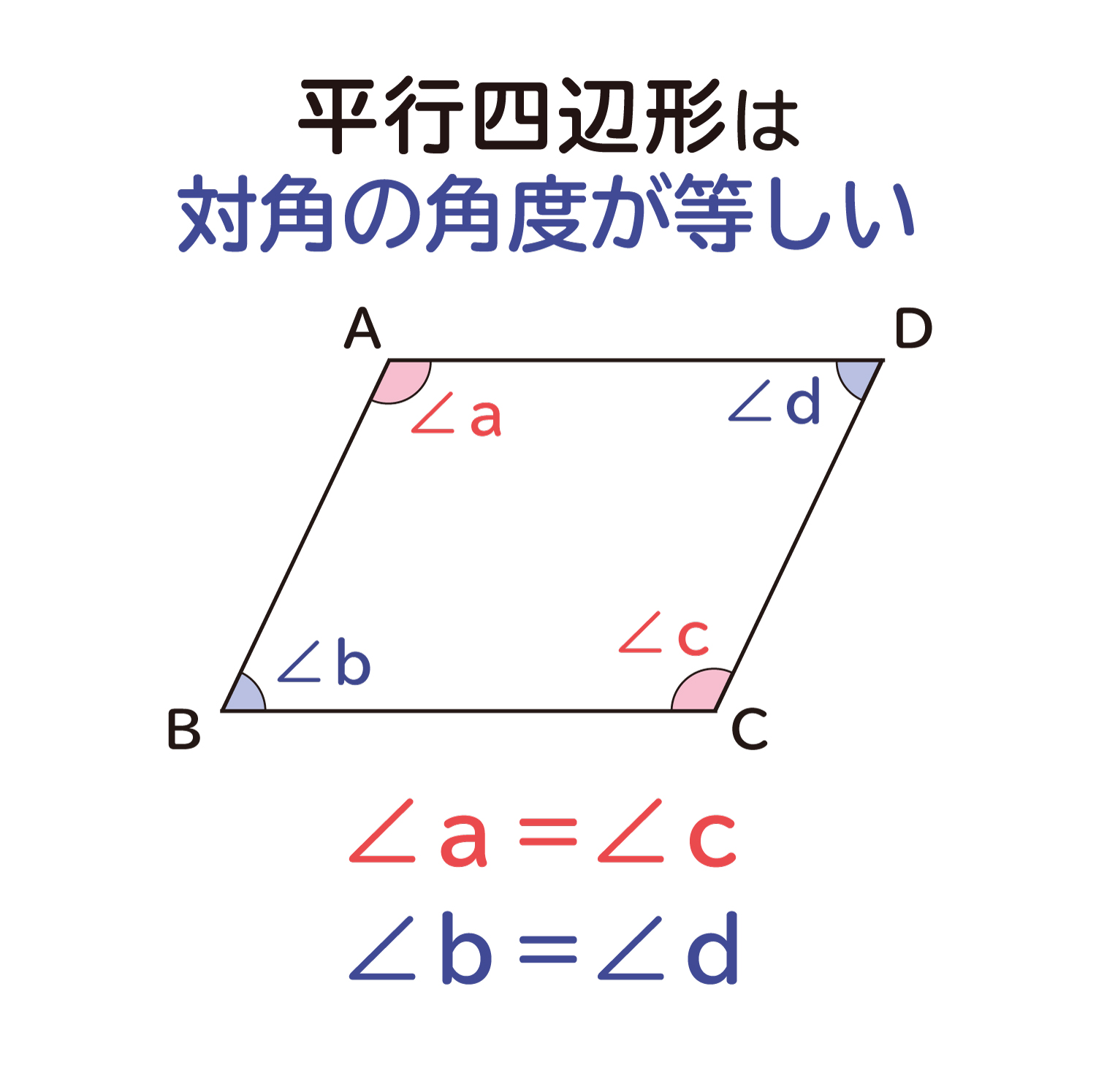



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル



平行四辺形になる条件
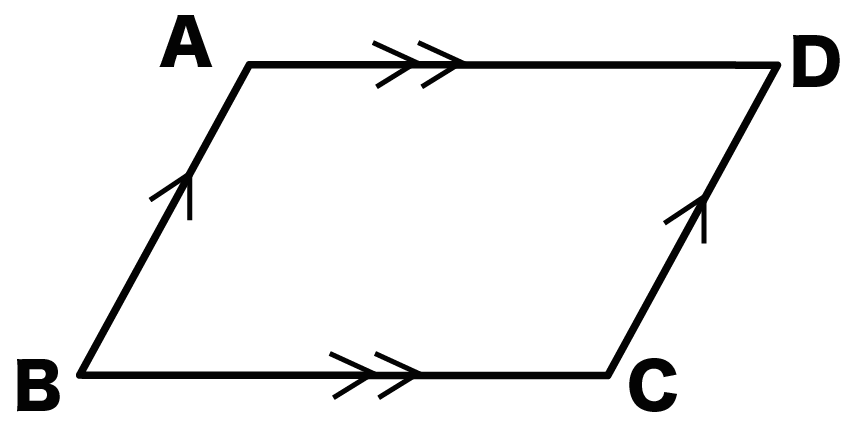



3分でわかる 平行四辺形の定義とは Qikeru 学びを楽しくわかりやすく




ファイル 平行四辺形の面積2 Png Wikibooks




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



平行四辺形の角の二等分線
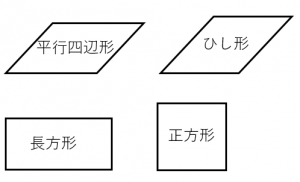



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット
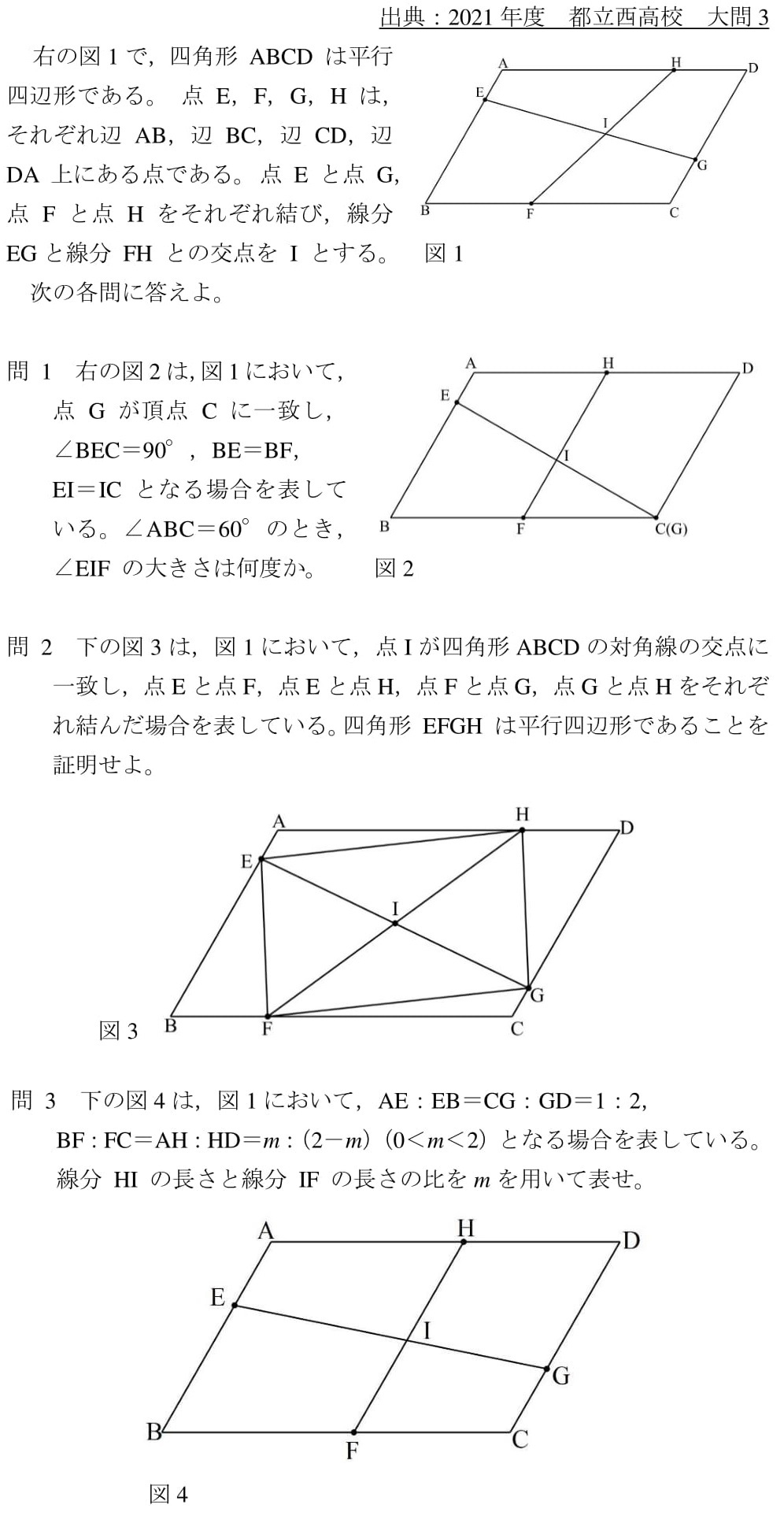



21都立西 平行四辺形の難問証明 高校入試 数学 良問 難問




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ
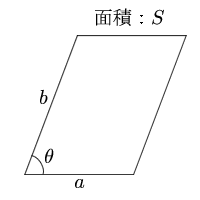



平行四辺形 2辺と間の角度 面積の計算 計算サイト




高校数学b ベクトルの成分表示と平行四辺形 受験の月
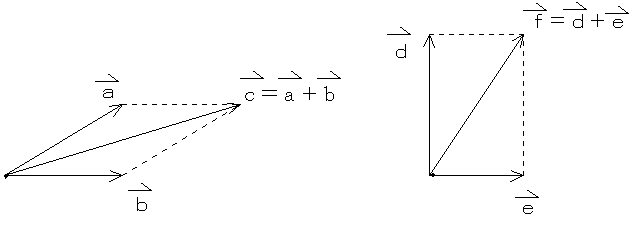



力の平行四辺形


