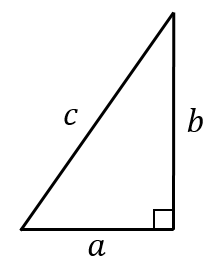
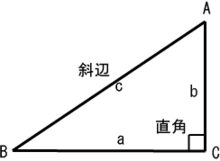
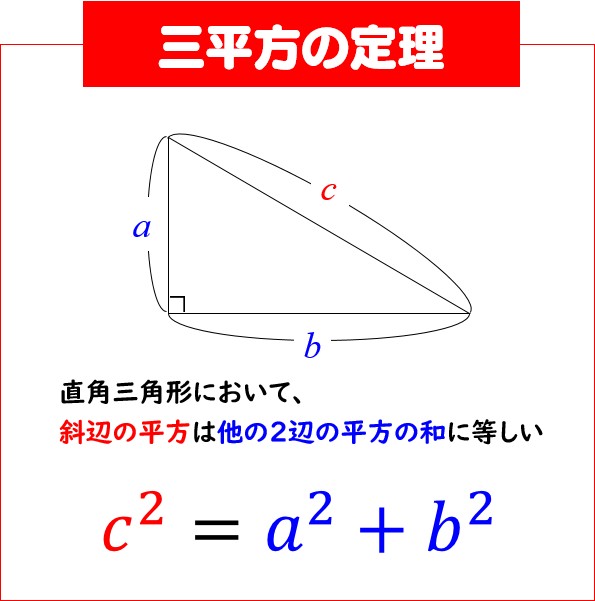
②三角形の3辺の長さがわかっているとき、直角三角形かどうかを判定することができる。 ③三平方の定理を用いて目的とする辺や線分の長さを求めることができる。 (4)数量、図形等についての知識・理解 ①三平方の定理とその逆を理解する。直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /三平方の定理 上図のように,直角三角形ABCの直角を挟む2辺の長さを,a, b, 斜辺の長さを c とすると, 辺の長さの間に次の関係式が成り立つ。 これを,「三平方の定理」または「ピタゴラスの定理」という。 ※ 「斜辺」とは,直角に対する辺で,直角

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
三平方の定理 直角三角形 辺の長さ
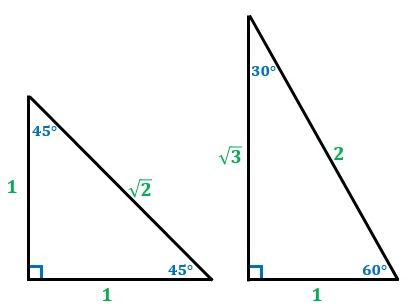
三平方の定理 直角三角形 辺の長さ-初等幾何学における ピタゴラスの定理 ( ピタゴラスのていり 、 ( 英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理 ( さんへいほうのていり ) 、 勾股弦の 直角二等辺三角形の辺の比は、必ず「 \color {red} {1 1 \sqrt {2}} 」 となります。 1 辺の長さからほかの辺の長さを簡単に求められるので、この比は必ず覚えておきましょう。 なぜこの比が成り立つかは、 三平方の定理 から示すことができます。 三平方の




三平方の定理 おやじさん ネット
三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。三平方の定理_座標平面の三角形 座標上の2点A,Bの距離 A (x1, y1),B (x2, y2)とすると 線分ABの長さ = (x 1 x 2) 2 (y 1 y 2) 2 A B x y O
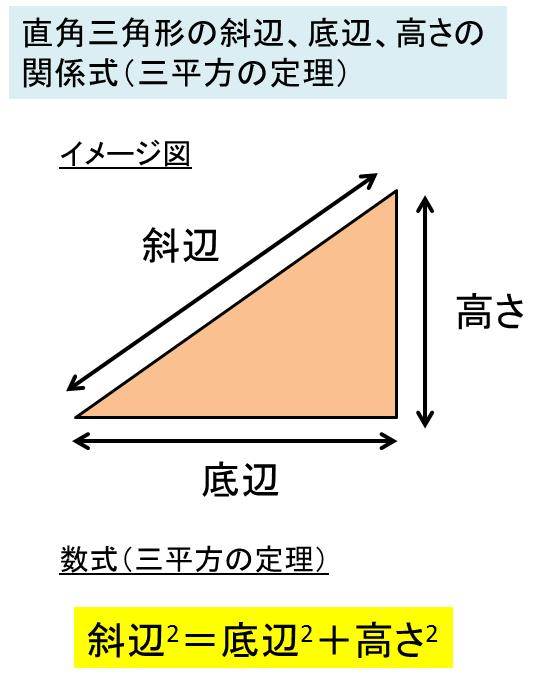
■次のような直角三角形の三辺の長さについては, a 2b 2=c 2 が成り立ちます.(これを三平方の定理といいます.) ■逆に,三辺の長さについて, a 2b 2=c 2 が成り立つとき,その三角形は直角三三平方の定理三平方の定理直角三角形の \(3\) 辺の長さには、以下のようの関係式が常に成り立ちます。\(a^2 b^2 = c^2\)※直角三角形の \(3\) 辺で、最も長い辺は直角の向かいの辺で、この辺を斜辺といいます。上の三角形の斜辺は、長さが \(Ccm\) の辺です。三平方の定理の求め方や特別な直角三角形の辺の長さの割合についてノートにまとめる。 3 / 4 時 ねらい ・ 弦の長さを、三平方の定理を使って求めることができる。
中学数学 三平方の定理の内容 z 三平方の定理とその証明 z 直角三角形の辺の長さ z 三平方の定理の逆 z 三平方の定理の応用(平面図形、空間図形など) *「ページ表示」を「見開き」でご覧いただきますと、問題とその 答えが見やすくなります。直角三角形の一辺の長さを入力 辺 a = 3 辺 b = 4 辺 c = 5000 直角三角形の一辺の長さを入力 辺 a = 45 辺 b = 102 辺 c = このように直角三角形の斜辺の長さを計算してみました。 その他のサンプルプログラムも合わせてご覧ください。下の三平方の定理の証明の方法について,太郎さんと花子さんが考えています。あとの(1), (2)の各問いに答えなさい。 三平方の定理 直角三角形の直角をはさむ2辺の長さを a,b, 斜辺の長さをc とすると,次の関係が成り立つ。 a 2+ b = c



1




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
直角三角形の定義とさまざまな公式 レベル ★ 基礎 平面図形 三角比・三角関数 更新日時 直角三角形 とは,1つの角が直角である三角形のことです。 直角三角形のさまざまな性質を紹介します。 目次 三平方の定理(ピタゴラスの定理)STEP1 三平方の定理とは 直角三角形ABCの辺ABの長さをc、辺ACの長さをb、辺BCの長さをaとします。 このとき、直角と向かい合う辺ABを斜辺といい、31 三平方の定理 ここでは,直角三角形の辺の長さの関係について学習してみましょう。 A三平方の定理(ピタゴラスの定理) 直角三角形の直角をはさむ2 辺の長さをa,bとし,斜辺の 長さをcとすると a2 +b2 =c2 が成り立つ。




感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社



直角三角形で 3辺の比が整数になる例25個と作り方 具体例で学ぶ数学
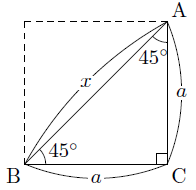
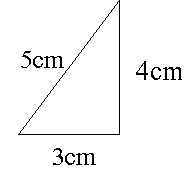
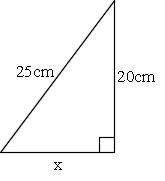
直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。 よって、直角二等辺三角形の辺の比は「1:1;√2」です。 三平方の定理 は ピタゴラスの定理 、 勾股弦 こうこげん の定理 とも呼びます。 この定理は、 直角三角形の3つの辺の長さの関係 を表しています。 上図の直角三角形では、直角を挟む2つの辺の長さがa、bで、斜辺の長さがcとなっています。三平方の定理を利用して,線分の長さを求めることができる 問1.次の各直角三角形で、三平方の定理を使って,残りの辺の長さを求めなさい。 (1) (2) (3) 問2.次の の値を求めなさい。x (1) (2) (3)



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube
=== 三平方の定理の逆 === 《解説》 ■次のような直角三角形の三辺の長さについては, a 2b 2=c 2 が成り立ちます.(これを三平方の定理といいます.) ■逆に,三辺の長さについて, a 2b 2=c 2 が成り立つとき,その三角形は直角三角形です.左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64 三平方の定理とは 直角三角形のときに利用できる 辺の長さの関係式でしたね。 それを発展させて考えていくと 直角三角形だけでなく 鋭角、鈍角三角形を見分ける方法として活用することができます。 入試などでは、活用する機会は少ないと思います




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



直角三角形の辺の長さ 合同条件 面積について アタリマエ
となる. 南海 そう. われわれの平面で普通に距離といっているものは, 2点 の間の距離 が, その2点を結ぶ線分を斜辺とするような直角三角形 の, 直角を挟む2辺 の長さを用いて上のように表される. 三平方の定理はこれを主張している.直角三角形の辺の長さ 解説 次のような直角三角形ABCでは,三平方の定理より, a 2 b 2 =c 2 という関係が成り立つので,三平方の定理を用いることで,直角三角形の2辺の長さから残りの1辺の長さを求めることができます。 三平方の定理では、特別な直角三角形辺の比を使って、三角形の辺の長さなどを求めることが出来ます。 基本事項をしっかり覚えて、素早く計算出来るように練習することが大切になります。 基本事項 次の3つの直角三角形の辺の比を覚えてください。




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座




数学 中3 61 三平方の定理 基本編 Youtube




三平方の定理の証明と使い方



三角定規の3辺の比 まなびの学園



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三平方の定理で辺を求める Youtube




三平方の定理の証明と使い方




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




無料 中3数学 発展 応用問題 問題プリント 334 三平方の定理2




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




三角形の各辺が3 4 5のとき直角三角形である理由 図付き なぜか分かる はかせちゃんの怪しい研究室




直角三角形の辺の長さ 合同条件 面積について アタリマエ




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 1 4




三平方の定理 覚えておきたい基本公式を解説 数スタ




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典



見本pdf 新中学問題集 発展編 塾用教材 教育開発出版株式会社 Scm H S3 Mihon




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
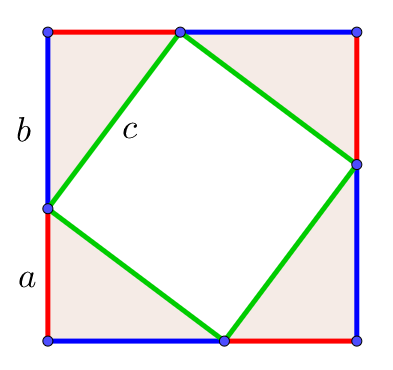



三平方の定理の証明2 4つ直角三角形と真ん中の四角 キソカラ




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学




特別な直角三角形の辺の比 無料で使える中学学習プリント




三平方の定理 覚えておきたい基本公式を解説 数スタ




無料 中3数学 発展 応用問題 問題プリント 333 三平方の定理1




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



直角三角形の辺の比 東久留米 学習塾 塾長ブログ




三平方の定理 ピタゴラスの定理 と公式の証明 忍者が用いた三角の知恵 アタリマエ




エレガント直角 三角形 の 定理 最高のカラーリングのアイデア




三平方の定理 ピタゴラスの定理




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




三平方の定理の証明と使い方




3 4 5の三角形で 本当に直角ができる Note Board




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく




特別な直角三角形の辺の比 無料で使える中学学習プリント




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




練習22がわかりません 三平方はわかりますがのこりのものがわかりません Clear



Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



三角形の性質




直角三角形の辺を求める Youtube




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



直角二等辺三角形の辺の長さは 1分でわかる求め方 公式 辺の長さと角度の関係 証明




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題




カーナビはなぜ正確なの その秘密 三平方の定理 で教えます 横山 明日希 ブルーバックス 講談社 2 4



リンクの図に示すように 長方形の中に直角三角形が2つあります ある程度わかっている寸法をもとに短辺abの長さを求めると どういう値になりますか Quora




三平方の定理の証明 直感的に分かる図で解説します 数学fun




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




三平方の定理の応用




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ Youtube




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



3




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



Mathematics 三平方の定理 2 特別な直角三角形 働きアリ




15 75 105 165 の三角比 数学i フリー教材開発コミュニティ Ftext




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



三平方の定理




直角三角形の辺の長さ 合同条件 面積について アタリマエ




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




三平方の定理の利用 1 きっずゼミ子育て応援ブログ




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト



質問コーナー Discuss Scratch




Mathematics 三平方の定理 2 特別な直角三角形 働きアリ



1




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



三平方の定理の証明 直感的に分かる図で解説します 数学fun




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



1
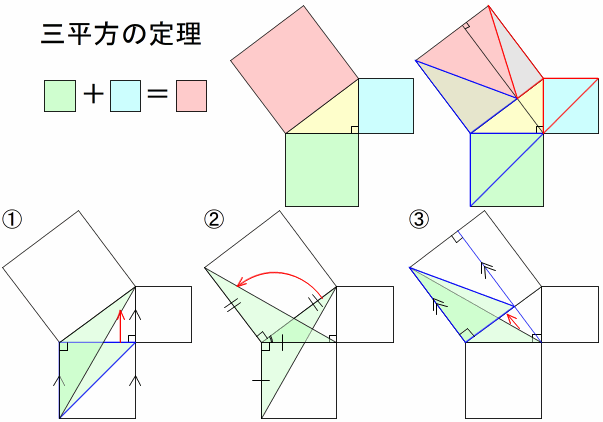



3 4 5の三角形で 本当に直角ができる Note Board




三角形の3辺の長さから高さ 面積を求める 高校入試問題 数学 を毎日解いてみよう




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
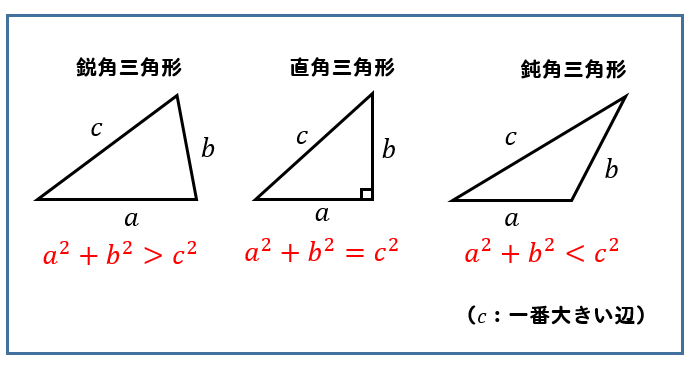



鋭角 鈍角三角形 三平方の定理を使って見分ける方法を解説 数スタ




三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく




三平方の定理 おやじさん ネット



Http Www Edu Tens Net Kyouikuken Basic Takamatsu Pdf Jsanques S9 07 Pdf
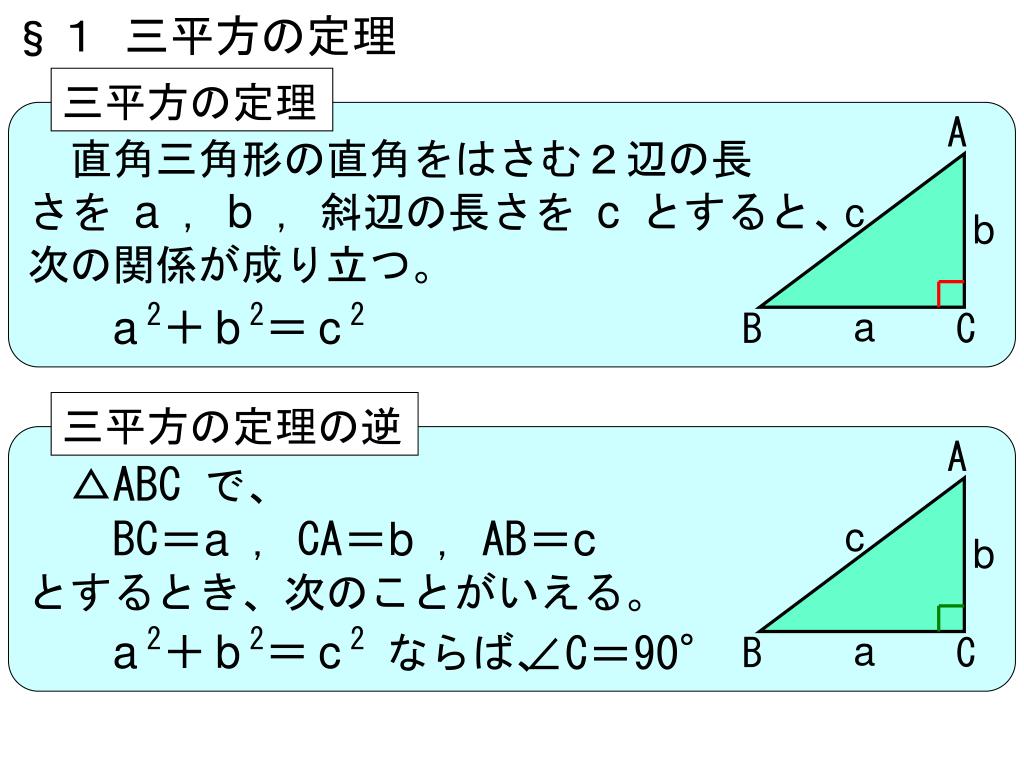



Ppt 6 三平方の定理 Powerpoint Presentation Free Download Id



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学



直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




Ai家庭教師laf先生 質問回答中 Su Twitter 証明シリーズ 三平方の定理 直角三角形の斜辺の長さをc 残りの二辺の長さをそれぞれaとbとおくと C 2 A 2 B 2 なんで と思った人も多いかと思ったので 実際に証明してみました 理解できた人rt T



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生


